Hello It's good to be back ^_^
파이썬 머신러닝 스터디 6주차 (ch06 차원 축소) 본문
교재: 파이썬 머신러닝 완벽 가이드
공부한 페이지 : pp. 399-
실습한 내용: https://github.com/HongYeonLee/Pylot_MachineLearningStudy
GitHub - HongYeonLee/Pylot_MachineLearningStudy
Contribute to HongYeonLee/Pylot_MachineLearningStudy development by creating an account on GitHub.
목차
01. 차원 축소 (Dimesion Reduction) 개요
02. PCA (Pricipal Component Analysis)
03. LDA (Linear Discriminant Analysis)
04. SVD (Singular Value Decompostion)
05. NMF (Non-Negative Matrix Ractorization)
01. 차원 축소 개요
차원 축소
- 매우 많은 피처로 이루어진 다차원 데이터 세트의 차원을 축소해 새로운 차원의 데이터 세트를 생성하는 것을 말한다
- 더 직관적으로 데이터를 해석하고 학습에 필요한 처리 능력도 줄일 수 있다
- 대표 알고리즘으로 PCA, LDA, SVD, NMF가 있다
- 피처 선택 (feature selection)과 피처 추출 (feature extraction)로 나눌 수 있다
피처 선택
- 특정 피처에 종속성이 강한 불필요한 피처는 아예 제거해 데이터의 특징을 잘 나타내는 주요 피처만 택하는 것을 말한다
피처 추출
- 기존 피처를 저차원의 중요 피처로 압축해서 추출하는 것을 말한다
- 기존 피처가 인지하기 어려웠던 잠재적인 요소를 추출하는 것을 의미한다
- ex) 모의고사 성적, 종합 내신성적, 수능성적, 봉사활동, 대회활동, 수상경력 등의 데이터를 학업 성취도, 커뮤니케이션 능력, 문제 해결력과 같은 데이터로 압축해서 추출할 수 있다
이미지와 텍스트 차원 축소
- 이미지-차원 축소를 통해 과적합이 일어날 확률을 줄인다
- 텍스트-차원 축소를 통해 문서 내 단어들의 구성에서 숨겨져 있는 시맨틱 (Sementic) 의미나 토픽(Topic)을 찾아낼 수 있다
02. PCA (Pricipal Component Analysis)
- 가장 대표적인 차원 축소 기법으로, 여러 변수간에 존재하는 상관관계를 이용해 이를 대표하는 주성분 (Pricipal Component)을 추출해 차원 축소하는 것을 말한다
- 가장 높은 분산을 가지는 데이터를 축으로 삼아 차원 축소한다
공분산
- 분산이 한 개의 특정한 변수의 데이터 변동을 의미했다면, 공분산은 두 변수 간의 데이터 변동을 의미한다
- Cov(X, Y) - X와 Y간의 공분산을 의미한다
공분산 행렬
- Squate matrix이며 Symmetric matrix이다
- 대각 원소는 각각의 데이터들의 개별 분산값을 의미한다

- 대각원소 3.0, 4.5, 0.91는 개별 원소 X, Y, Z의 각각의 분산을 의미한다
- 대각원소가 아닌 원소들은 각 데이터의들의 공분산을 의미한다
- ex) Cor(X, Y) = -0.71
공분산행렬이 Symmetric matrix이므로 고유벡터를 Orthogonal matrix로 가진다
| Orthogonal matrix - A^T = A^-1인 행렬 또는 AA^T = I인 행렬 |
따라서 공분산 행렬 C는 다음과 같이 분해할 수 있으며
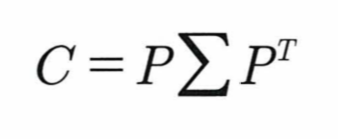
P = n x n 크기의 고유 벡터 othogonal mtx, ∑는 n x n 크기의 square mtx
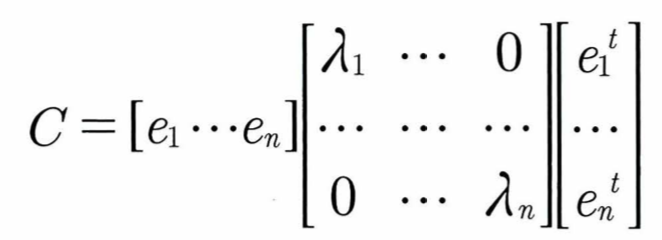
| 즉 공분산 행렬 C = 고유 벡터 othogonal mtx * 고유값 square mtx * 고유벡터 othogonal mtx의 transpose ei는 i번째 고유벡터를, λi는 i번째 고유벡터의 크기 e1은 가장 분산이 큰 방향을 가진 고유벡터이며 e2는 e1에 수직이면서 다음으로 가장 분산이 큰 방향을 가진 고유벡터 |
→입력 데이터의 공분산 행렬이 고유벡터와 고유값으로 분해될 수 있으며 이렇게 분해된 고유벡터를 이용해 입력 데이털르 선형으로 변환하는 것이 PCA방식이다

파이썬에서 PCA 방식 사용하기
- 여러 속성을 PCA로 압축하기 전에 각 속성값을 동일한 스케일로 변환해야 한다 - 사이킷런의 StandardScaler 이용
- 사이컷런에서 제공하는 PCA 클래스는 n_components(PCA로 변환할 차원의 수)를 입력받는다
- PCA객체의 explained_variance_ration_ 속성은 전체 변동성에서 개별 PCA 컴포넌트별로 차지하는 변동성 비율을 제공한다
from sklearn.preprocessing import StandardScaler //속성 스케일링
from.sklearn.decompostion import PCA //PCA 클래스 임포트
PCA(n_components = 정수)
PCA.fit(데이터)
PCA.transform(데이터)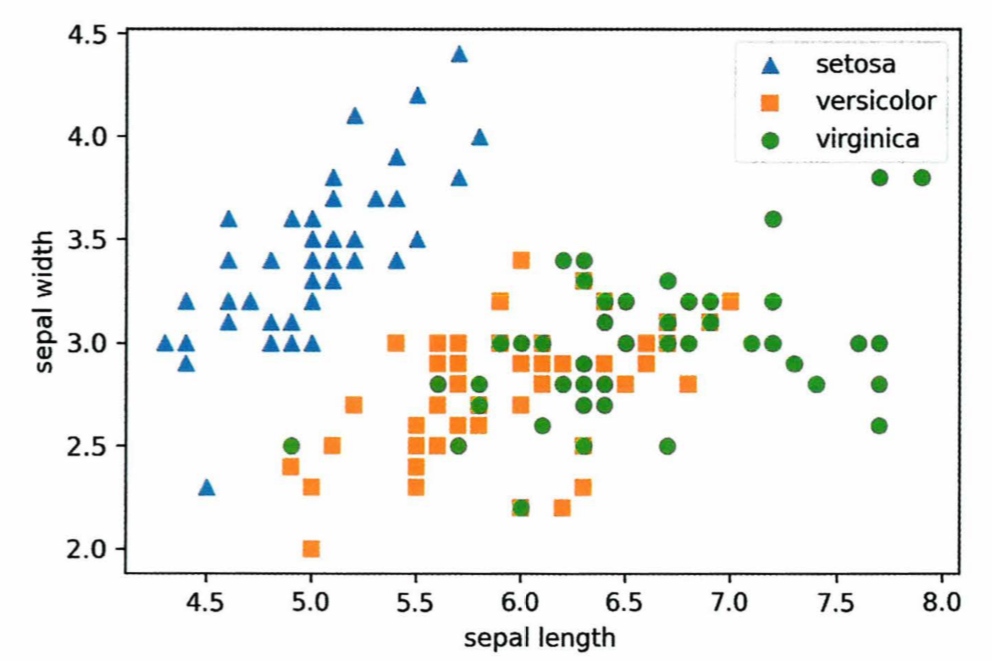
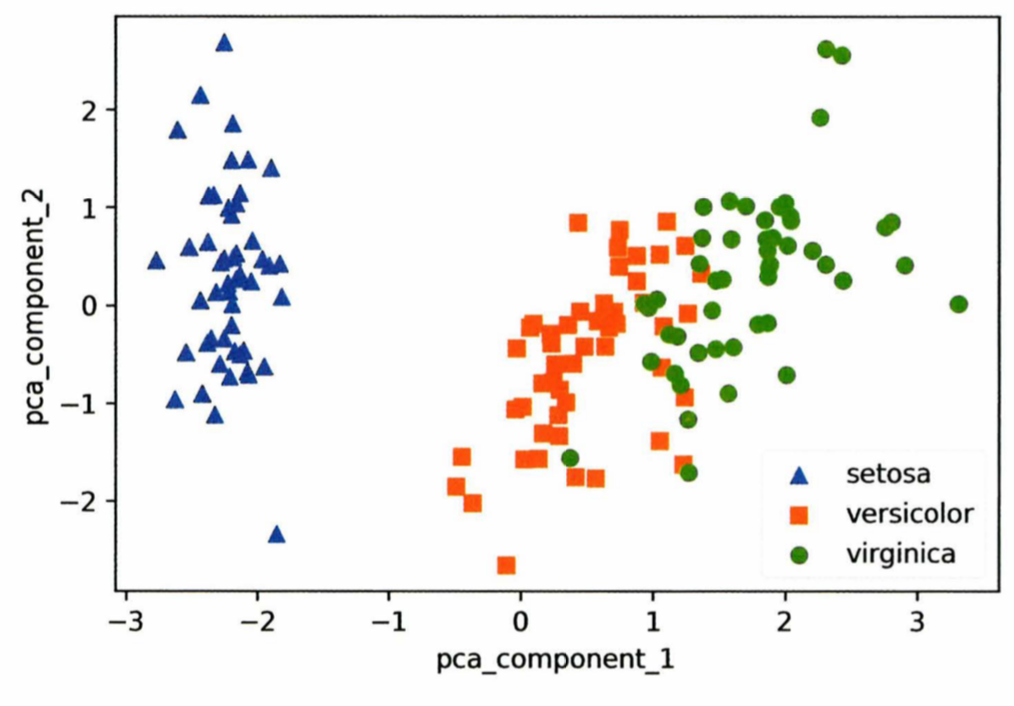
- 예시는 원본 피처 개수 4개에서 2개로 압축하여 차원 축소한 것으로, 예측 성능의 정확도가 8%정도 감소했지만,
- 원본 피처 개수 23개를 6개로 압축하여 차원 축소한 것은 예측 성능이 약 1~2%정도만 감소할 정도로 PCA는 뛰어난 압축능력을 가지고 있다
- PCA는 컴퓨터 비전 (Computer Vision) 분야에서 자주 사용되며 얼굴 인식에서 많이 사용된다.
03. LDA (Linear Discriminant Analysis)
'Study > 파이썬 머신러닝' 카테고리의 다른 글
| 파이썬 머신러닝 스터디 8주차 (ch08 텍스트 분석) (1) | 2024.05.23 |
|---|---|
| 파이썬 머신러닝 스터디 7주차 (ch07 차원 축소) (0) | 2024.05.14 |
| 파이썬 머신러닝 스터디 5주차 (ch05 회귀) (0) | 2024.05.04 |
| 파이썬 머신러닝 스터디 4주차 (ch04-2 분류) (0) | 2024.04.11 |
| 파이썬 머신러닝 스터디 3주차 (ch04-1 분류) (2) | 2024.04.04 |



