Hello It's good to be back ^_^
파이썬 머신러닝 스터디 5주차 (ch05 회귀) 본문
교재: 파이썬 머신러닝 완벽 가이드
공부한 페이지 : pp. 308-
실습한 내용: https://github.com/HongYeonLee/Pylot_MachineLearningStudy
GitHub - HongYeonLee/Pylot_MachineLearningStudy
Contribute to HongYeonLee/Pylot_MachineLearningStudy development by creating an account on GitHub.
github.com
목차
01. 회귀 소개
02. 단순 선형 회귀를 통한 회귀 이해
03. 비용 최소화 하기 - 경사 하강법((Gradient Descent) 소개
04. 사이킷런 LineaRegression을 이용한 보스턴 주택 가격 예측
05. 다항 회귀와 과(대)적합/과소적합 이해
06. 규제 선형 모델 - 릿지, 라쏘, 엘라스틱넷
07. 로지스틱 회귀
08. 회귀 트리
01. 회귀 소개
지도학습
- 분류
- 회귀
회귀분석
- 데이터 값이 평균과 같은 일정한 값으로 돌아가려는 경향을 이용한 통계학 기법
회귀
- 여러 개의 독립변수와 한 개의 종속변수 간의 상관관계를 모델링하는 기법
- ex) 아파트의 방 개수, 방 크기, 주변 학군 등은 독립변수, 이에 따른 아파트 가격은 종속 변수라고 볼 수 있다
- Y = W1*X1 + W2*X2 + .... + Wn*X* (Y는 종속 변수, Xn은 독립변수 Wn은 회귀 계수)
회귀 계수
- 머신 러닝 관점에서 피처는 독립변수에 해당, 결정 값은 종속 변수에 해당
- 주어진 피처와 결정 값 데이터 기반에서 학습을 통해 최적의 회귀 계수를 찾아내는 것이 머신 러닝의 회귀 예측
| 회귀 계수의 선형 여부 | 선형 회귀 | 비선형 회귀 |
| 독립변수의 개수 | 단일 회귀 | 다중 회귀 |
선형 회귀
- 가장 많이 사용되며, 실제 값과 예측 값의 차이(오류의 제곱 값)를 최소화하는 직선형 회귀선을 최적하는 방식
선형 회귀의 종류


02. 단순 선형 회귀를 통한 회귀 이해
단순 선형 회귀
- 독립변수와 종속변수가 하나인 선형 회귀를 말한다
- ex) 주택 가격을 주택의 크기로만 결정된다고 할 경우
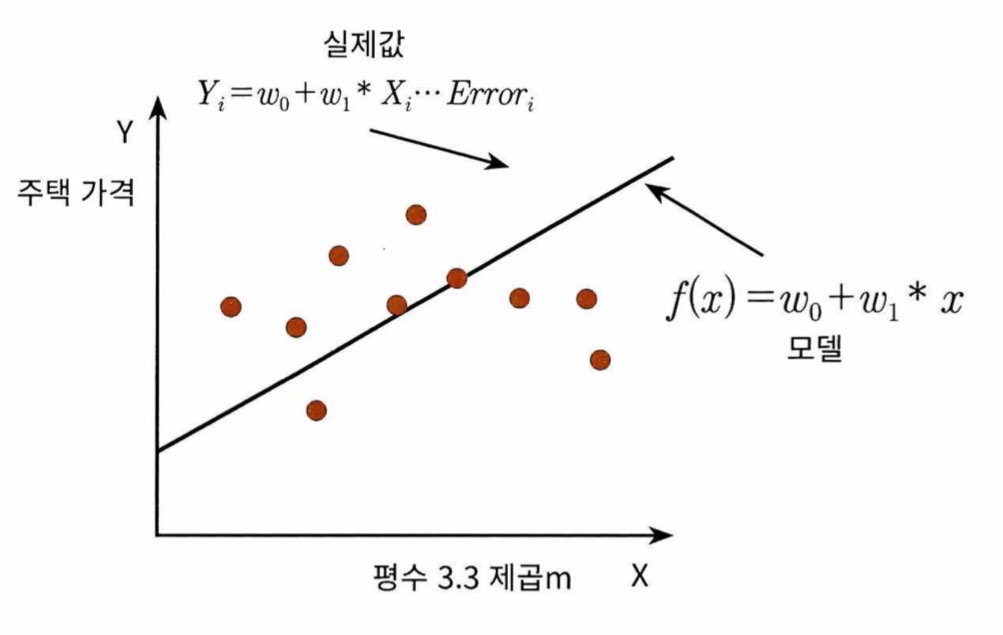
| 독립변수(Y)가 1개, 종속변수 (X)가 1개 이므로 단순한 1차 함수로 나타낼 수 있다 실제 주택 가격은 이러한 1차 함수에서 실제 값만큼의 오류 값을 빼거나 더한 값이 된다 즉, 실제 주택 가격 = w0 + w1*X + 오류 값 이러한 실제 값과 모델 값의 차이를 오류 값을 남은 오류, 잔차라고 부른다 최적의 회귀 모델을 만드는 것은 이러한 잔차의 합 (오류의 합)이 최소가 되는 모델을 말하는 것을 의미한다 (= 오류 값의 합이 최소가 될 수 있는 최적의 회귀 계수를 찾는다) |
오류 합
- 절댓값을 취해 더하거나 (Mean Absolute Error), 오류 값의 제곱해서 더하는 방식 (RSS, Residua Sum of Square)이 있다
- 일반적으로 RSS의 방식을 이용한다
- 이에 따라 RSS는 변수 w0와 w1으로 표현되며 이러한 RSS를 최소하기 위한 최적의 w0, w1을 학습을 통해 찾는 것이 머신 러닝 기반 회귀의 핵심
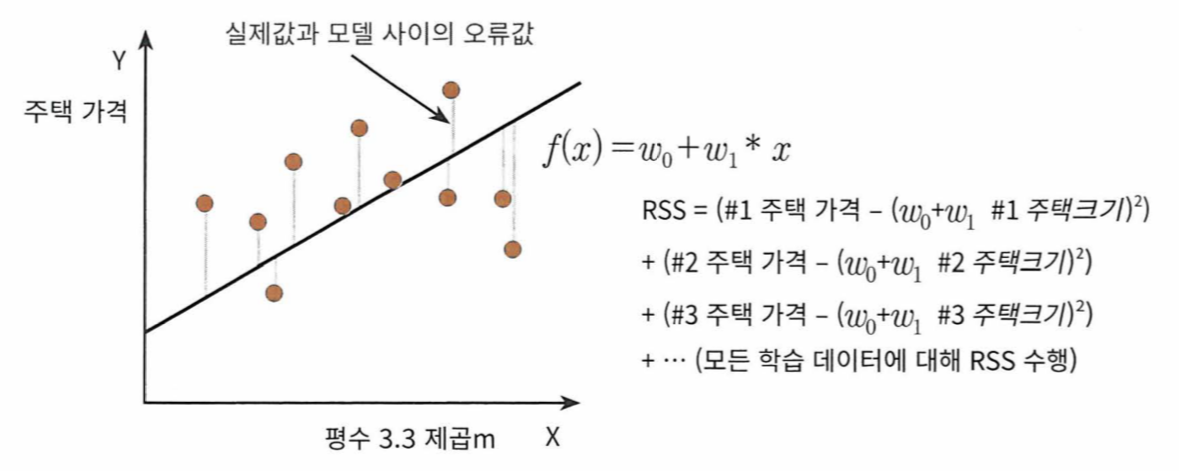
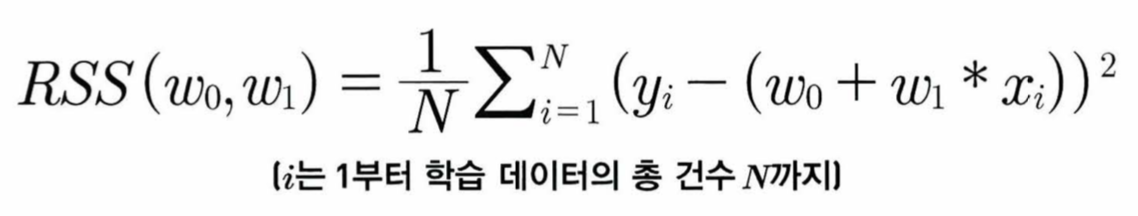
| yi 는 실제 값 w0 + w1*x는 예측 값 RSS = 1/총 데이터 건수 {(1번 실제 값 - 1번 예측 값)^2 + (2번 실제 값 - 2번 예측 값)^2 + ... + (n번 실제 값 - n번 예측 값)^2} |
- 이러한 RSS를 비용(cost)라고 부르며 w 변수 (회귀 계수)로 구성되는 RSS를 비용 함수라고 부른다
- 이러한 비용 함수가 리턴하는 값(=오류 합)을 지속적으로 감소시키고 최종적으로는 더이상 감소하지 않는 최소의 오류 값을 구하는 것이 머신 러닝의 핵심
- 비용 함수를 손실 함수라고도 부른다
03. 단순 선형 회귀를 통한 회귀 이해
경사하강법
- 반복적으로 비용함수(RSS)의 리턴값(= 오류 값 = 예측 값과 실제 값의 차이)이 작아지는 방향성을 가지고 W 파라미터를 계속해서 보정해 나가는 방법
- 위의 RSS 수식에서 RSS의 최솟값이 되는 w0, w1를 찾기 위해선 RSS를 편미분 (변수가 2개이므로)하고, 그렇나 온 편미분 값을 반복적으로 보정하여 w0, w1값을 업데이트하면 RSS(=R(w))가 최소가 되는 w0, w1을 구할 수 있다.
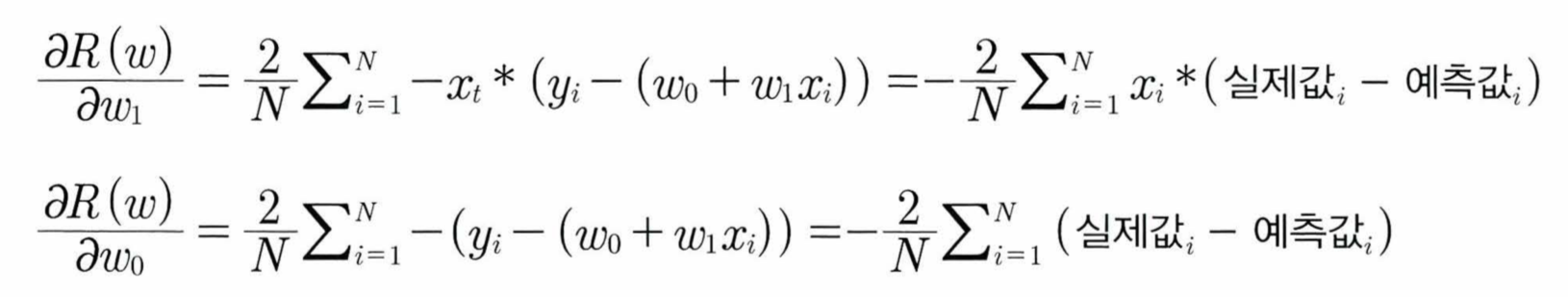
- 편미분 값이 너무 커지는 것을 방지하기 위해 보정 계수를 곱하는 데 이 보정 계수를 '학습률'이라 한다
경사하강법의 순서

파이썬 코드로 구현하기
import numpy as np
//비용 함수를 구하는 함수
def get_cosf(y, y_pred):
N = len(y)
cost = np.sum(np.square(y - y_pred))/N //비용 함수 수식
return cost
//w0, w1을 업데이트하는 함수
def get_weight_updates(w1, w0, X, y, learning_rate = 0.01):
y_pred - np.dot(X, w1.T) + w0 //dot()은 넘파이의 내적 연산
diff = y-ypred
w0_factors = np.ones((N.1))
w1_update = -(2/N)*learning_rate*(np.dot(X.T, diff))
w2_update = -(2/N)*learning_rate*(np.dot(w0_factors.T, diff))
return w1_update, w2_update
//입력 인자 iters로 주어진 횟수만큼 반복적으로 w0, w1에 업데이트 적용하는 함수
def gradient_descent_steps(X, y, iters = 10000):
for ind in range(iters):
w1_update, w0_update = get_weight_updates(w1, w0, X, y, learning_rate = 0.01)
w1 = w1 - w1_update
w0 = w0 - w0_update
return w1, w0
- 경사하강법은 모든 학습 데이터에 대해 반복적으로 비용함수 최소화를 위한 값을 업데이트하기에 시간이 굉장히 오래 걸린다
- 따라서 대부분 확률적 경사 하강법이나 미니 배치 확률적 경사 하강법을 이용한다
(미니 배치) 확률적 경사 하강법
- 일부 데이터만 이용해 w가 업데이트 되는 값을 계산한다
- 경사 하강법으로 구한 w1, w0와 큰 차이가 없다
피처가 여러개일 경우
다음과 같이 예측 회귀식을 세울 수 있다
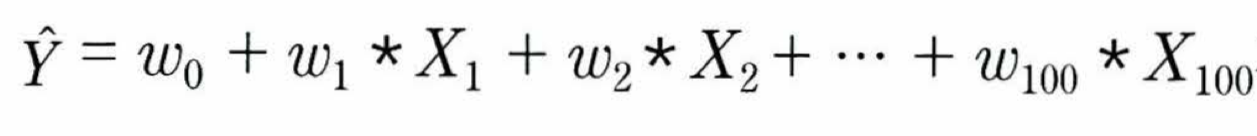
예측 행렬(y_pred) 또한 위에서 구한 것과 같이
Y = np.dot(X, W(의 Transpose)) + w0로 구할 수 있다
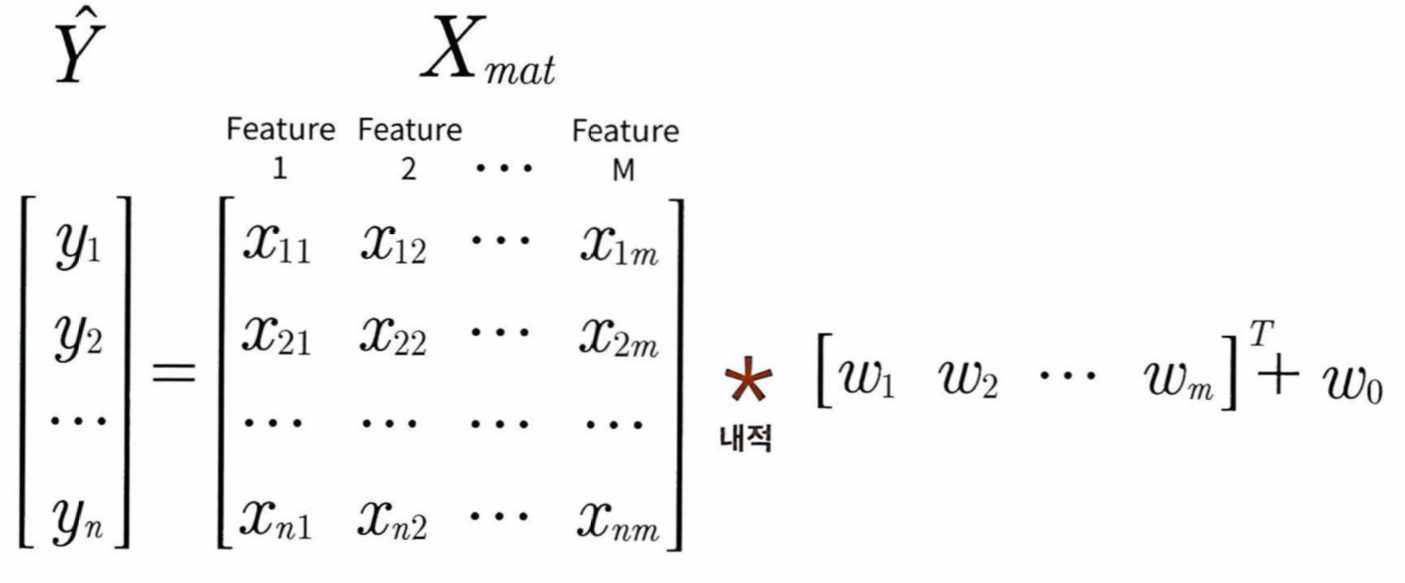
w0를 W 배열에 내에 포함하기 위해 Xmat에 1값을 가진 열벡터를 추가해도 된다
LinearRegression 클래스
예측값과 실제 값의 RSS를 최소화해 OLS(Ordinary Least Squares) 추정 방식으로 구현한 클래스
fit() 메서드로 X, y 배열을 입력받으면 회귀계수인 W를 coef_ 속성에 저장한다
class sklearn.linear_model.LinearRegression(fit_intercept = True, normalize = False, copy_X = True, n_jobs = 1)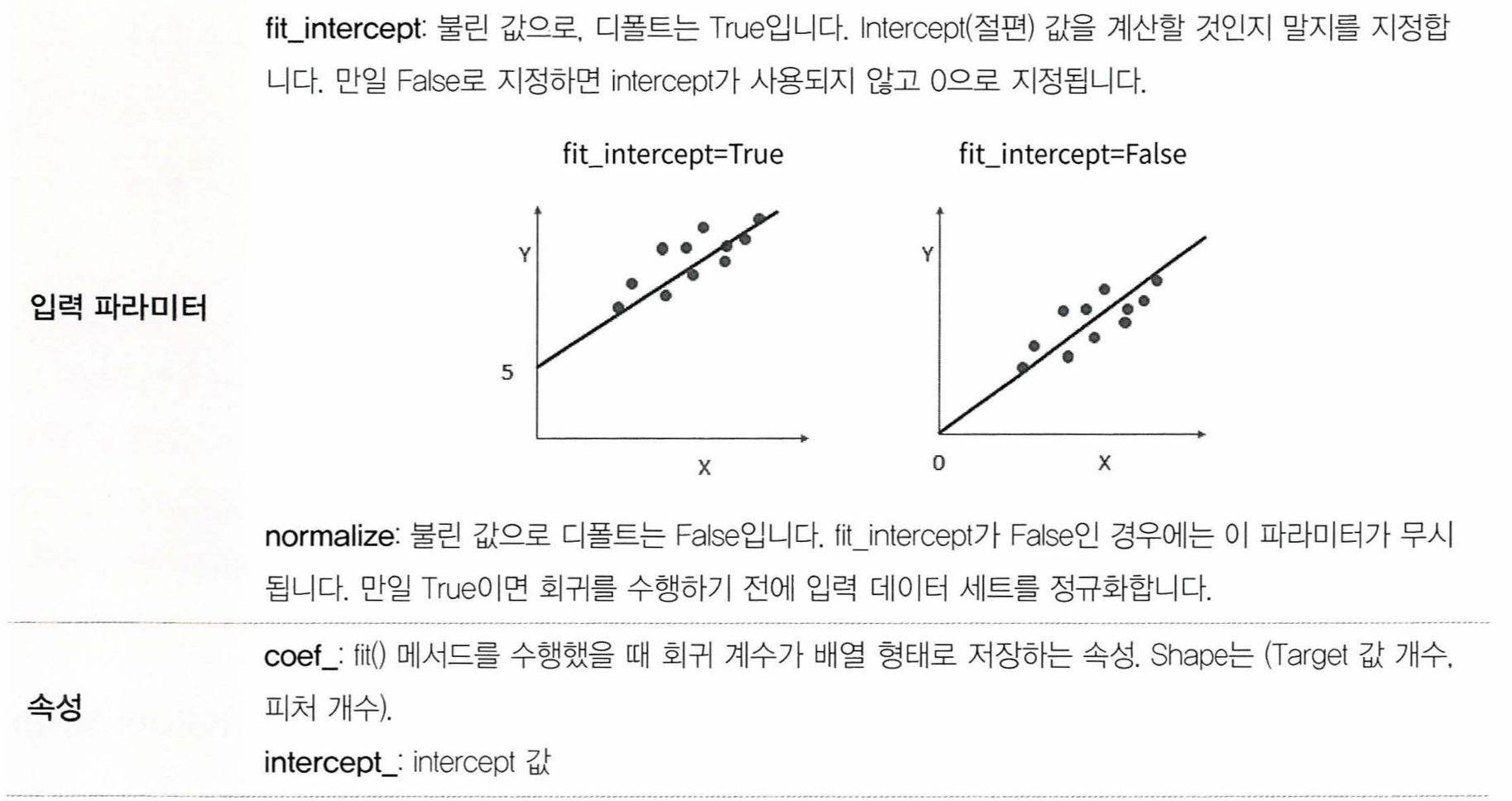
Ordinary Least Squares
- 입력 피처의 독립성에 영향을 많이 받는다
- 피처간의 상관관계가 높을 경우 분산이 매우 커져서 오류에 매우 민감해짐 = 다중공선성(multi-collinearity) 문제
- 이런 경우 독립성적인 중요 피처만 남기고 제거하거나 규제를 적용한다.
- 또는 PCA를 통해 차원 축소를 수행할 수도 있다
회귀 평가 지표
'Study > 파이썬 머신러닝' 카테고리의 다른 글
| 파이썬 머신러닝 스터디 7주차 (ch07 차원 축소) (0) | 2024.05.14 |
|---|---|
| 파이썬 머신러닝 스터디 6주차 (ch06 차원 축소) (0) | 2024.05.08 |
| 파이썬 머신러닝 스터디 4주차 (ch04-2 분류) (0) | 2024.04.11 |
| 파이썬 머신러닝 스터디 3주차 (ch04-1 분류) (2) | 2024.04.04 |
| 파이썬 머신러닝 스터디 2주차 (ch03 평가) (1) | 2024.03.28 |




